THE LOGIC OF CAUSATION

THE LOGIC OF CAUSATION

Phase Two: Microanalysis

Chapter 14–Main Three-ItemSyllogisms

1. Applying Microanalysis to Syllogism

2. The Moduses of Premises

3. The Moduses of Conclusions.

4. Dealing with Vaguer Propositions.

1. Applying Microanalysis to Syllogism.

We shall now begin to use microanalytic methods for the understanding and solution of syllogistic problems. In this way, we shall develop an advanced and general theory of the syllogism, using a tool more powerful and universal than any previously used. Ciao Aristotle, hello future logic. We shall proceed in stages, from the simpler cases to the more complex.

As we are already aware, syllogism basically involves three items (terms or theses) in three propositions. The propositions (in this context, of causative form) are the major premise, the minor premise and the conclusion. The items involved are the minor item (which occurs somewhere in the minor premise, and as the cause in the conclusion), the major item (which occurs somewhere in the major premise, and as the effect in the conclusion), and the middle item (present in both premises, but ignored in the conclusion).

Syllogism, then, is argument aimed at discovering or establishing the relation (the conclusion) between two items (the minor and major), by way of their given relations (the premises) to a third item (the middle). If the premises are compatible, they will either imply a certain conclusion, in which case the syllogism is ‘valid’; or fail to imply any conclusion, in which case the syllogism is ‘invalid’.

And as we have seen, there are three main ‘figures’ for such argument, traditionally labeled Nos. 1, 2 and 3. In the first figure, the middle item has the roles of effect in the minor premise and cause in the major premise; in the second figure, it has the role of effect in both premises; and in the third figure, it has the role of cause in both figures.

Ordinarily, the three items occur only in the positions just said. But we may conceive of special cases where the items recur in other positions, as complements. This gives rise to arrangements we have called ‘subfigures’. We need not concern ourselves with these complications at this stage, but will only focus our attention on the essential, Aristotelian arrangements.

Figures are, of course, abstractions regarding the positions of the items. Syllogism is concretized in individual formal ‘moods’, when the exact relations between these items are specified – i.e., in the present context, the determination and polarity of the causative relation in each premise. The latter are likewise useless without specification of the figure involved.

Thus, to end this brief review, we will here to begin with reexamine, using the microanalytic method, three-item causative syllogism in the three main figures (without consideration of the fourth figure or of subfigures). We shall start with positive moods, i.e. moods with both premises affirmative; after that, we shall deal with negative moods, i.e. those involving at least one negative premise.

Still later, we shall gradually treat all other conceivable situations, and thus demonstrate the universality of this technique.

Now, putting aside all the above mentioned details, syllogism is nothing more than a logicalconjunctionof two propositions (the premises), and all we seek through it is an evaluation or inference of theirintersection(the conclusion). That is:

The major premise + the minor premise = the conclusion (if any).

It follows that,knowing the moduses of the premises, we can ascertain those of the conclusion. The conclusion may thus be viewed as a summary the information of the premises taken together; i.e. as a statement of their combined value in knowledge. Each premise, taken separately, has a certain value – expressed in its modus list; in the conclusion, we find out their mutual impact – which is merely their common moduses, if any. We can refer to an image in mechanics, we have two vectors and we wish to calculate their resultant force.

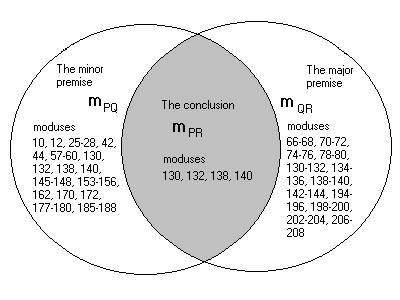
The following simple example will illustrate how a valid conclusion arises. Mood 1/m/m(which, you will recall, we labeled 155) consists of the premises “Q is a complete cause of R” (the major, which we may labelm_QR) and “P is a complete cause of Q” (the minor, which we may labelm_PQ). We know by macroanalysis that its conclusion is “P is a complete cause of R” (which we may labelm_PR); as shown in the table below, microanalysis yields the same result.

Table 14.1.Microanalysis of a mood – the example of mood 1/m/m(No. 155).

Note that the premises, being in the first figure, have respectively forms QR (major) and PQ (minor), while the conclusion must be of form PR. Once the modus or moduses of the premises are ascertained (as explained in the next section), we need only find our which modus or moduses, if any, they have in common. The form or forms which includeallsuch common modus(es) is/are implied by them, and may be considered as constituting the conclusion. This intersection may be illustrated as follows (Diagram 14.1):

In our example, four moduses are found in common. With reference to Table 12.4 of the chapter on systematic microanalysis, which concerns causative propositions of form PR, we see that these four moduses are allamongthe 36 alternatives ofm. It follows thatm_PRis our conclusion or part thereof. Continuing our search, we see thatnot allof these four moduses are included inmn(only No. 132 is so) ormq_abs(only Nos. 132, 138, 140 are so), therefore we cannot obtain a more precise positive conclusion. Thus,m_QR+m_PQism_PR.

Note wellthat, to concludem_PR, we do not need to find all its moduses to be in common to the premises – just one would suffice; what is important is that all the moduses which are in common to the premises be included in the list of 36 for that putative conclusion.

Also note thatthe above mentioned table[1], which enumerates three-item moduses for propositions of form PR, is appropriate for evaluatingthe conclusion, which has that same form in all figures.

But the moduses ofthe premisescannot be identified with reference to that table, since they have forms other than PR, namely QR or PQ (in the first figure). In their case, we must revert to the grand matrix for three items, i.e. the preceding table in the same chapter, Table 12.3. How this is done is explained in detail in the next section, where the results for all conceivable strong or absolute weak premises in whatever figure are also tabulated.

We can, at the outset, formulate the following generalrules of inference, based on our knowledge of the intersection process:

1.If the premises havenomodus in common, they are incompatible. This signifies that the premises are already incoherent and cannot credibly occur together in knowledge. If we encounter such premises (without common modus, inconsistent) in practice, as often happens, not only can we draw no conclusion from them, but one or both of them must be reviewed and rejected or corrected.

2.If the premises haveone or moremodus(es) in common and such modus(es) is/areallincluded by some causative propositional form(s), the latter constitute(s) our conclusion. Note well again that, though all common moduses of the premises must be moduses of the putative conclusion, not all the moduses of the latter need be common to the former. For a form, remember, is implied by any one of its alternative moduses. Also note, a conclusion may consist of one causative form or a conjunction of such forms, of whatever polarities.

3.But if the premises havetwo or moremoduses in common and these moduses arenotallincluded by some causative propositional form(s), though some of them are included by a form and others by its contradictory, we have no conclusion. In this case, the premises are indeed compatible, since they have common moduses; but those common moduses do not give rise to a causative proposition, however vague, being too scattered[2]. The common moduses may of course still give rise to a proposition of form other than causative; but this is not of interest in the present context.

2.The Moduses of Premises.

In order to systematically apply the microanalytic method to the solution of syllogistic problems, we need first to identify the moduses of all conceivablepremises. For we already have the moduses of eventualconclusions, which always have form PR: these are given in Table 12.4 of the chapter on systematic microanalysis.

It is marvelous thatwe can refer to the same grand matrix for three items, with 255 possible moduses, which we used to interpret three-item propositions, to interpret three-item syllogisms. For syllogisms with four items, we shall need to consider 65,535 possible moduses![3]

Regarding the premises in the three figures, we see that they involve four possible pairs and arrangements of items, namely QR or RQ for the major premise and PQ or QP for the minor premise. The summary moduses of the various generic forms of interest to us here are as follows. Note well that in the following table, the weak determinationsp,qare intended asabsolute, though not so specified.

Table 14.2.Three-item summary moduses for strong or absolute weak generic positive premises.

Where two letters (among a-h) appear in two cells of a column, the intent is to indicate that this pair of cells can never both be zero, i.e. a ‘µ‘ is intended[4]. Thus, for instance, instead of writingµ_ae, I write ‘ae’ in both rows a and e. This is done just to improve visibility of the information.

Notice the following details in the above table. First, note the similarity of sequence of modalities in two columns read in opposite directions (for instance the modus ofm_QRread from top to bottom and that ofn_QRread from bottom to top); this signifies mirroring. Second, note the identity of moduses of various pairs of propositions, likem_QRandn_RQ, orp_QRandq_RQ; this signifies convertibility from one to the other.

We can now, with reference to the rules implied by the above table, easily read the grand matrix for three items[5]in the usual manner, to obtain the alternative moduses of all the premises of concern to us here. For now, we need only deal with positive premises – first, the generics, based on the above summary moduses; then, the joint determinations, by recourse to intersections between the generics. The results are as follows:

Table 14.3.Enumeration of three-item alternative moduses for strong or absolute weak positive premises, generic or joint, for any figure of syllogism.

To repeat, the same information for causative propositions of form PR has already been tabulated, in a previous chapter; and those results are applicable to reading conclusions. The above table concerns positive premises which may arise in three-item syllogism. Though the same propositional form has always the same number of moduses, the modus numbers differ according to the items involved and their positions. Note this well, and compare and contrast.

Next Section(continuation of same chapter)